¿Cómo estimar la flecha en estructuras de hormigón armado? En este artículo explicaremos cómo calcular dos tipos de deformada, la instantánea o inicial y la total a largo plazo. Y en ambos casos, el resultado lo conseguiremos interpolando las deformadas que hallemos para las inercias bruta y fisurada de la sección estudiada.
E.L.S. y control de deformaciones según Código Estructural
El control de deformaciones en el Código Estructural se describe en el anejo 19 apartado 7.4, de Control de deformaciones. El punto 6 nos indica que el estado de deformaciones puede comprobarse mediante:
- Método 1: Limitación de la relación canto-luz, queda desarrollado en el artículo 7.4.2 del anejo 19, y es de aplicación directa (es decir, no se calcula la deformada y por ello no se desarrolla en este post);
- Método 2: Comparación de la deformación calculada con un valor limite, queda desarrollado en el apartado 7.4.3, e incluye dos variantes: método general y simplificado.
Método General
Debido a la finalidad práctica de este blog, y la complejidad del cálculo mediante este método (por factores como el comportamiento no lineal del hormigón, fisuración, deformaciones diferidas, historial de cargas, etc.), solo se dejará planteada su expresión teórica, para posteriormente centrarnos en el método simplificado.
Integración de la ley de curvaturas: y» = c = M / (E x I)
Donde:
- M: Momento flector
- E: Módulo de Elasticidad
- I: Inercia
Además, la ley de curvaturas (c) estará siempre entre dos estados extremos, que son:
- Estado I: Sección no fisurada (colaboración en tracción del hormigón)
- Estado II: Sección fisurada (sin colaboración en tracción del hormigón)
Método simplificado
El método se ajusta a lo señalado por el Código Estructural. Hallaremos por un lado la deformada instantánea y por otro lado la deformada total o a largo plazo, pero previamente deberemos conocer las inercias brutas y fisuradas de la sección que estudiemos.
Inercia bruta
Para una sección rectangular de hormigón, el módulo de inercia es: Ib = b x h3 / 12
Pero si la sección tuviera una forma irregular (en T, por ejemplo), podríamos hallar su módulo de inercia siguiendo el teorema de Steiner, cuyos pasos están desarrollados en la primera parte de este post previo
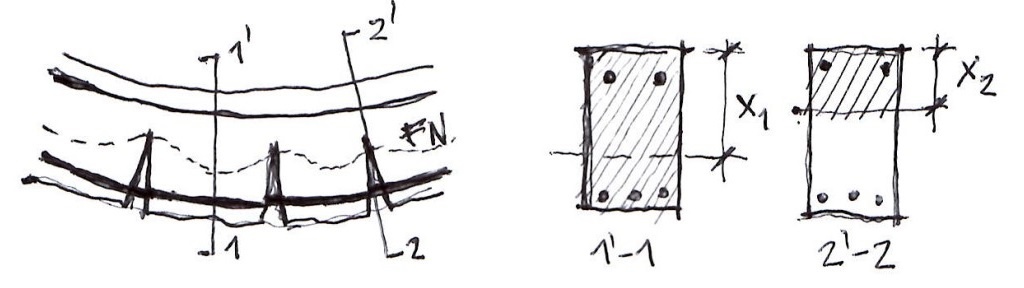
Inercia fisurada
La obtención de la inercia fisurada no es tan directa, para ello primeramente tendríamos que obtener la profundidad de la fibra neutra “x” respecto a la cara superior de la viga, que para una sección rectangular se obtiene despejando «x» de la siguiente igualdad:
0,5 b x2 + αe (As + A’s) x – αe (dAs + d’A’s) = 0
Donde:
- b: base de la viga (mm)
- αe: relación entre módulo de elasticidad del acero y del hormigón (Es/Ecm)*
- A’s: cuantía de acero en cara superior (mm2)
- As: cuantía de acero en cara inferior
- d´: espesor de recubrimiento (mm)
- d: canto mecánico (mm) o distancia a borde superior desde armadura inferior
* para hallar αe podemos tomar como Es un valor aproximado de 200.000 N/mm2 y para Ecm recurriremos a la tabla 19.3.1 del anejo 19 del Código Estructural, o bien directamente a la expresión:
Ecm = 22000 [(fck + 8) / 10]0,3 N/mm2
Una vez hallado el valor de la profundidad de la fibra neutra «x», lo introduciremos en la siguiente expresión para hallar el valor de la inercia fisurada (If):
If = b x3 / 12 + αe As (d – x)2 + αe A’s (d’ – x)2
Flechas instantáneas para inercia bruta y fisurada
Para calcular la flecha, en primer lugar deberemos asignar una carga de estudio «q», que hallaremos según los parámetros señalados en el CTE DB SE.
Procedemos a obtener la flecha instantánea para los estados I y II (como ejemplo, señalaremos el caso de una viga biempotrada con carga uniformemente repartida):
Flecha para inercia bruta: δI = qL4 / (384 Ecm Ib)
Flecha para inercia fisurada: δII = qL4 / (384 Ecm If)
Flecha instantánea
La flecha instantánea se calcula mediante una interpolación, que obtenemos de la siguiente expresión:
δinst = ζ δII + (1 – ζ) δI
Para ello, deberemos despejar ζ, que se considera el coeficiente de participación del hormigón traccionado en la sección, que sería igual a cero en el estado I (no fisurado), y que para el resto de casos se obtiene mediante la expresión:
ζ = 1 – β (σsr / σs)2
Donde:
- β = 1,0 en casos de carga de corta duración
- β = 0,5 en casos de carga prolongada o de un gran números de ciclos de carga (y que es la cifra que tomaremos habitualmente en edificación)
- σsr: Tensión en la armadura de tracción calculada, considerando la sección fisurada, para toda la carga
- σs: Tensión en la armadura de tracción calculada, considerando la sección fisurada, para la carga que produce la primera fisura
Nota importante: Se puede sustituir la relación (σsr / σs) por una relación (Mcr / M) o (Ncr / N), siendo Mcr el momento de fisuración y Ncr el axil de fisuración, lo que puede simplificar el cálculo, porque:
Mcr = fctm b h2 / 6
y:
fctm = 0,30 fck 2/3 (fck y fctm en N/mm2)
Aplicando estas fórmulas, se comprueba que una vez superado el estado I (no fisurado) las flecha final interpolada tiende a acercarse rápidamente a las flechas del estado II, puesto que el valor de ζ aumenta exponencialmente.
Flecha total o a largo plazo
En el caso de cargas con una duración suficiente como para dar lugar a la aparición del fenómeno de fluencia, la deformación total, incluida la fluencia, puede calcularse utilizando el módulo elástico efectivo del hormigón, mediante la siguiente expresión
Ec,eff = Ecm / [1 + φ (∞,t0)]
Hallaremos φ (∞,t0) en las tablas de la figura A19.3.1 del Código Estructural :
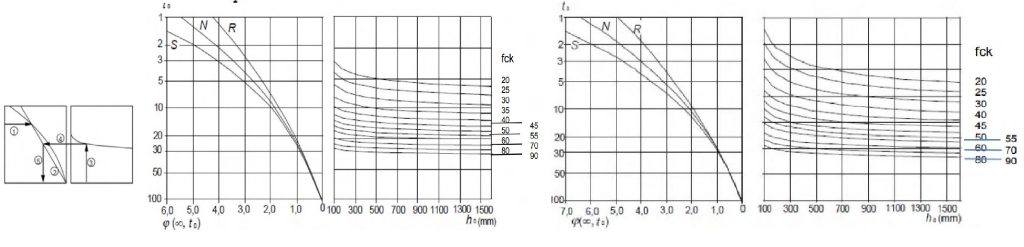
Para el uso de las tablas previas y hallar el coeficiente φ (∞,t0) hay que tener en cuenta que:
- se debe seguir el orden de pasos señalados en el esquema situado a la izquierda
- el tiempo de entrada t0 se expresa en carga se estima en días,
- h0 es el cociente entre volumen de hormigón en la sección, y áreas expuestas,
En cualquier caso, para condiciones normales, no nos equivocaremos demasiado si en las estructuras situadas en climas con humedad relativa cercana al 80% (tablas de la izquierda) damos un valor de φ (∞,t0) cercano o ligeramente inferior a 2,0; y en las estructuras en climas secos e interiores, con una humedad relativa cercana al 50% (tablas situadas a la derecha) damos un valor de φ (∞,t0) entre 2,0 y 2,5.
Como anteúltimo paso, hallaremos las flechas para el estado I (sin fisurar) y estado II (fisurado) con la misma formulación que en la flecha instantánea, si bien sustituyendo Ecm por Ec,eff:
Flecha para inercia bruta: δI tot = qL4 / (384 Ec,eff Ib)
Flecha para inercia fisurada: δII tot = qL4 / (384 Ec,eff If)
Para terminar, al igual que en el caso de la flecha instantánea, también debemos interpolar:
δtot = ζ δII,tot + (1 – ζ) δI,tot
Comprobación respecto a valores límite
El objetivo de hallar las flechas, más allá de el interés por obtener una cifra concreta, reside en comprobar el cumplimiento de la norma. Si el marco normativo de aplicación es el Código Técnico (CTE DB SE) y el Código Estructural encontraremos que:
En primer lugar deberemos comprobar que no superamos los valores máximos para la deformada a largo plazo, que serían los señalados en el CTE (con un límite de deformada vertical de L/300 -CTE DB SE 4.3.3.1-, más restrictivo que el L/250 genérico que expresa el Código Estructural -Anejo 19, punto 7.4.1.4-). Por lo tanto:
δtot < L/300
En segunda lugar, deberemos comprobar que la flecha diferida (entendida como la resta entre la flecha total y la instantánea, no supere L/500 – Código Estructural, Anejo 19, punto 7.4.1.5-).
δdif = δtot – δinst < L/500
En una futura entrada desarrollaremos la justificación del cumplimiento del ELS a través de la limitación de la relación canto-luz, desarrollada en el 7.4.2 del Anejo 19, cuya aplicación es más sencilla que la del método aquí desarrollado.



