En estructuras de gran luz y poco peso es bastante habitual que nos podamos encontrar con problemas por la entrada en resonancia del conjunto. El origen del problema está en las cargas dinámicas que soportan estos elementos.
Hay casos muy conocidos como los del puente de Tacoma, en Estados Unidos, o el de la pasarela del Milenio, en Londres, pero hay muchos más, y no necesariamente tan espectaculares.
El puente de Tacoma fue el tercer puente colgante más largo de Estados Unidos cuando se construyó (1940), sólo superado por el Golden Gate y el puente George Washington. Durante su construcción ya se detectaron movimientos inesperados, y tras su puesta en uso, apenas pasó medio año hasta que los vientos provocaran una entrada en resonancia de la estructura que terminó derivando en su colapso. Lo importante es que los vientos que provocaron el derrumbe no fueron especialmente fuertes, dado que la velocidad estimada aquel día fue de 40 mph (unos 64 km/h), sino que fueron los justos para provocar un aleteo que coincidió con la frecuencia natural del puente.
En el caso de la Pasarela del Milenio, en Londres, el caso no llegó a tanto. Este es el primer puente que se construyó para cruzar el Támesis desde la City en cien años (el anterior fue el puente de la Torre de Londres, en 1894). Su diseño, de Foster + Partners, Arup y Anthony Caro buscaba una gran esbeltez, que permitiera enmarcar las vistas de St Paul al cruzarlo, y no queriendo competir con el entorno circundante.
El día de su inauguración, en junio del 2000, las numerosísimas personas que acudieron para su estreno, provocaron un fenómeno que se ha venido en denominar excitación lateral sincrónica. Este efecto surge de una sincronización inicial fortuita que provoca una vibración en el puente. En ese momento, y de cara a poder mantenerse en pie sobre el puente, las personas sincronizaron su paso con la oscilación del puente, reforzando aún más dicha vibración.
Los diseñadores del puente, para solventar este fenómeno, y para evitar alterar la estética del mismo, en vez de rigidizar el puente (lo que supondría un cambio sustancial en su geometría), decidieron disipar la energía de oscilación mediante un complejo sistema de amortiguadores situado bajo su tablero.
No son estos los únicos casos, este es un fenómeno que puede suceder también en edificación convencional, sobre todo cuando vamos a grandes luces en acero. Y como lo normal es que no dispongamos de sistemas de amortiguación añadidos a nuestros diseños, lo más conveniente resulta ser asegurarse que la frecuencia de vibración de nuestros diseños sean adecuadas.

Estimación previa de límites de vibración en el diseño estructural:
Las vibraciones dependen de la luz, de la inercia de las piezas estructurales y de la masa a movilizar. El CTE DB SE señala que las frecuencias de las estructuras deben alejarse de las frecuencias de acción dinámica para evitar los fenómenos que hemos visto antes. El CTE no señala una determinación como tal para uso residencial, pero se establecen frecuencias de 8Hz para polideportivos o gimnasios, de 7Hz en salas de fiesta y de 3,4 Hz en locales de espectáculos con asientos fijos.
La exclusión de un mínimo en uso residencial es segura, en tanto que la vibración está íntimamente relacionada con la inercia y por ello con la deformación de las estructuras. Por lo que habitualmente, si un forjado cumple a flecha según el CTE, cumple también a vibración en casos en los que no se prevean acciones dinámicas importantes, como es en el caso del uso de vivienda.
Estudio del modo de vibración:
Para establecer preventivamente que los límites de vibración estén lejos de los valores que queramos establecer como límite, se puede realizar el estudio del modo de vibración de las piezas de la estructura. En el caso más sencillo, la frecuencia de vibración de una viga biapoyada puede establecerse como:
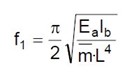
siendo:
- E: Módulo de elasticidad
- Ib: Módulo de inercia (se puede considerar el de la sección mixta, si la hubiera)
- m: masa por unidad de longitud, incluyendo el % casi permanente de la sobrecarga de uso
- L: Luz de la viga biapoyada
Siendo así, habrá que aplicar un 30% de la carga de uso para los casos de vivienda (para el resto de casos, ver tabla 4.2 CTE DB SE).
Si tuviéramos vigas de sección e inercias variables, podríamos aplicar la inercia de Branson, y en el caso de vigas continuas, no es difícil establecer sus frecuencias de vibración a partir de un simple precálculo de la distribución de momentos de cálculo. Desarrollaremos estos dos casos algo más complejos, junto con un ejemplo completo de cálculo en un post que publicaremos en breve.



