Una de las diferencias de la nueva normativa del código estructural respecto a la EHE-08 la encontramos a la hora de realizar comprobaciones de estado límite último a punzonamiento.
Estas diferencias están resumidas en el documento “Avance de la Guía de Aplicación del Código Estructural a la edificación” publicado por Juan Carlos Arroyo Portero y Alejandro Calle García.
A continuación, se explicará el cálculo a punzonamiento en losas según el código estructural:
Desarrollo teórico del cálculo de la resistencia a punzonamiento
El procedimiento de cálculo del punzonamiento se basa en las comprobaciones en dos puntos diferenciados:
- Comprobación en la cara del pilar
- Comprobación en el perímetro crítico u1.
Además, si es necesaria la armadura de punzonamiento, deberá encontrarse un perímetro exterior uout,ef, a partir del cual no sea necesaria la utilización de armadura.
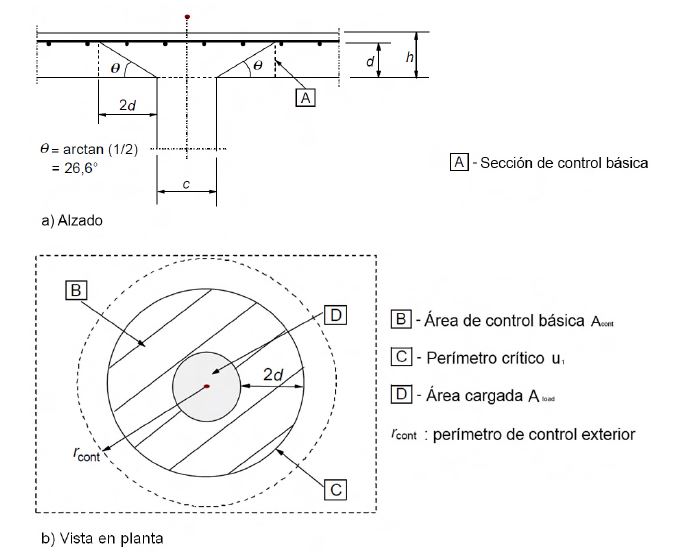
En el caso de perímetros afectados por el borde de una losa, habría que aplicar las siguientes directrices:
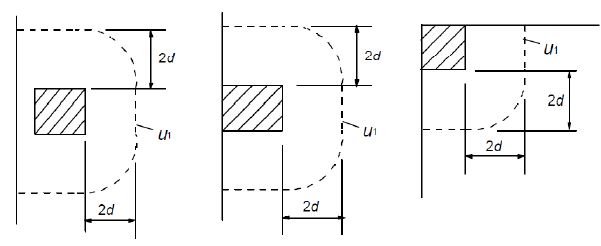
La tensión tangencial máxima de punzonamiento se tomará como:
𝜈Ed = (β x VEd) / (u1 x d)
donde:
d es el canto útil medio de la losa
u1 es la longitud del perímetro de control considerado
β coeficiente con los siguientes valores aproximados, según figura A19.6.21 del CE, para estructuras en las que la estabilidad lateral no dependa de que la losas y pilares trabajen como pórticos y las luces de los vanos adyacentes no difieran más de un 25%.
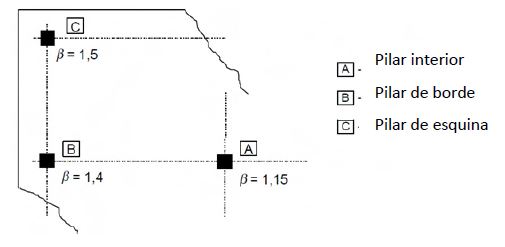
Comprobación en la cara adyacente al pilar
La resistencia a punzonamiento estará limitada por un valor máximo establecido mediante:
VEd = (β x VEd) / (u0 x d) < 𝜈Rd,max
Donde,
- u0 = perímetro del pilar (mm) para pilar interior
- u0 = c2 + 3d < c2 + 2c1 (mm) para pilar de borde
- u0 = 3d < c1 + c2 (mm) para pilar de borde
c1 y c2 son las dimensiones del pilar
β es el coeficiente descrito en el apartado anterior
𝜈Rd,max = 0,4 x 𝜈 x fcd donde ʋ se obtiene de la ecuación (6.6) del Anejo 19 del Código Estructural
𝜈 = 0,6 x [1 − (𝑓𝑐𝑘 / 250)]; con fck en N/mm2
Comprobación del perímetro crítico:
Losas sin armadura de punzonamiento
El valor de cálculo de la resistencia a punzonamiento en N/mm2 puede obtenerse de la siguiente expresión:
VRd,c = CRd,c k (100 ρl fck 1/2 ) 1/3 + k1 σcp > (𝜈min + k1 σcp)
Donde:
fck está en N/mm2
k = 1 + (200 / d) 1/2 > 2,0; con d en mm
ρl = ρlx ρly < 0,02; donde ρlx y ρly son las cuantías de armadura traccionadas adherentes en las dos direcciones. En cada dirección, la cuantía a considerar es la existente en un ancho útil igual a la dimensión del pilar sumándole tres veces el canto útil de la losa, 3d, a cada lado.
σcp = (σcy + σcz) / 2; donde σcy y σcz son las tensiones normales del hormigón en N/mm2 en la sección crítica en las direcciones respectivas.
CRd,c = 0,18 / ϒc
k1 = 0,1
𝜈min = 0,035 k 3/2 fck 1/2
Se debe comprobar la resistencia a punzonamiento de la base de los pilares a lo largo de los perímetros críticos situados dentro de una distancia 2d del perímetro del pilar, es decir, para la sección crítica de punzonamiento u1 definido anteriormente.
Losa con armadura de punzonamiento
En primer lugar se debe señalar que según el artículo 9.3.2 del anejo 19 una losa en la que se dispone de armadura de cortante debe de tener al menos un canto mínimo de 200mm. Esta novedad es sustancial, ya que impone unos cantos mínimos a las losas que previamente no existían.
En el caso de que se requiera armadura de punzonamiento, la resistencia se calculará según la siguiente expresión:
VRd,cs = 0,75 VRd,c + 1,5 (d/Sr) Asw fywd,ef (1/u1d) sen α < kmax VRd,c
Donde:
Asw es el área total de armadura de punzonamiento en un perímetro concéntrico al pilar en mm2
Sr es la distancia en la dirección radial entre dos perímetros concéntricos de armadura de punzonamiento
fywd,ef = 250 + 0,25 d < fywd; en N/mm2, resistencia de cálculo efectiva de la armadura de punzonamiento
d es la media de los cantos útiles en las direcciones ortogonales (en mm)
α es el ángulo entre la armadura de punzonamiento y el plano de la losa
kmax es un factor que limita la capacidad máxima que puede alcanzarse mediante la aplicación de la armadura de punzonamiento, cuyo valor es 1,5
VRd,c es un factor que limita la capacidad máxima que puede alcanzarse mediante la aplicación de la armadura de punzonamiento (ver en el punto anterior)
Se comprobará el perímetro crítico definido anteriormente, y además, se debe realizar una segunda comprobación para determinar el perímetro crítico exterior uout,ef para el cual no se requiere armadura de punzonamiento.
uout,ef = β x VEd / (VRd,c x d)
El perímetro de armadura de punzonamiento situado en la zona exterior, se debe situar a una distancia no mayor a kd, dentro del perímetro uout, donde k=1,5.
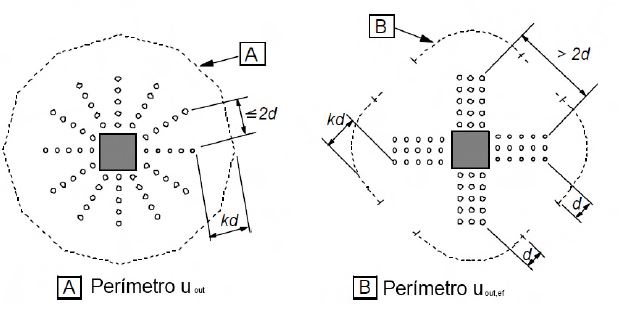
Consideraciones a tener en cuenta para la armadura de punzonamiento
Existen varias consideraciones que se han de tener en cuenta en cuanto al diseño de estas armaduras:
- Donde sea necesaria la armadura de punzonamiento, deberá disponerse entre el área o pilar cargado y un punto situado a una distancia kd, situado dentro del perímetro crítico en el que deja de ser necesaria la armadura de punzonamiento. Como mínimo, deberán disponerse dos perímetros de cercos, cuya separación no superará 0,75d.
- La separación de las ramas de los cercos a lo largo de un perímetro no debe superar el valor 1,5d dentro del perímetro (2d a partir del área cargada). En el caso de necesitar más armadura de punzonamiento, fuera del perímetro crítico, las ramas de los cercos no deberán tener una separación superior a 2d
- Para las barras dobladas dispuestas como se muestra en la siguiente imagen, se considerará suficiente la utilización de un único perímetro de cercos (ver figura A19.9.10 del CodE):
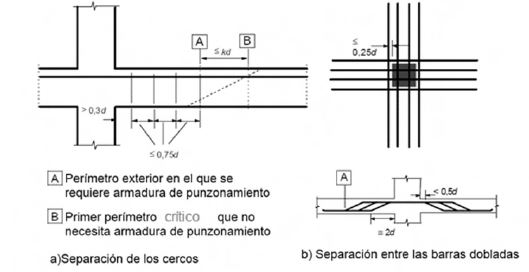
- En el cálculo sólo se puede incluir la componente vertical de las armaduras activas que pasen a una distancia no superior a 0,5d del pilar
- Las barras levantadas que atraviesan la zona cargada, o que pasan a una distancia inferior a 0,25d de la misma, pueden utilizarse como armadura de punzonamiento.
- La distancia entre la cara del soporte o el perímetro del área cargada y la armadura de cortante más cercana tenida en cuenta en el cálculo, no debe superar d/2.



