¿Qué es el módulo de balasto?
El coeficiente de balasto se define como el cociente entre la presión vertical aplicada en un determinado punto (q) y el asiento (s) que dicho punto experimenta.
Ks=q/s
Por lo tanto, el módulo de balasto nos permite calcular la interacción entre la cimentación de nuestro edificio y el terreno existente, y depende de esos dos factores, terreno y tipo de cimentación diseñada. Podríamos imaginarnos gráficamente este módulo como una base de infinitos muelles con una rigidez K situados bajo la cimentación de nuestro edificio.

La rigidez K varía en función del tamaño y geometría de la cimentación, dado que en función del tamaño de una zapata, el terreno movilizado puede tener mayor o menor profundidad. Se podría decir, como resumen, que el módulo de balasto es una propiedad del terreno ante un cimiento determinado.
Terzaghi, en la 1ª Conferencia de Mecánica de Suelos e Ingeniería de Cimentaciones (Harvard, 1936) enunció la importancia del bulbo de presiones y su relación con el cálculo de asientos. Recomendó tomar como Profundidad Significativa (PS) la que define la isobara de 0,2 Q para zapatas cuadradas y circulares, siendo Q la carga trasmitida por la zapata al terreno.
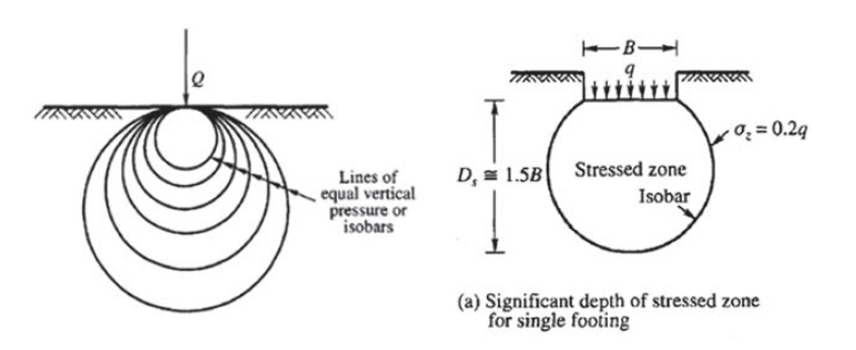
Habría que puntualizar que la rigidez K del terreno no sería la misma en todos los puntos bajo una viga corrida, dado que sería algo mayor en los extremos (en estas zonas se movilizaría menos volumen de terreno, generando deformadas inferiores a las del resto de los puntos centrales).
Siguiendo el mismo razonamiento, en una losa, la rigidez K variaría para cada uno de los puntos. Sin embargo, lo simplificamos y calculamos el asiento con un único módulo para toda la pieza, tengamos viga corrida, zapata o losa de cimentación. Ese módulo nos permitirá conocer el asiento global del conjunto calculado, pero no el de cada uno de sus puntos.

No hay requisitos de rigidez en los cimientos, salvo por control de asientos (CTE- DB- SE), y una vez salvado este condicionante previo, la rigidez que atribuimos al terreno respecto a nuestra zapata servirá sobre todo para posibilitar el cálculo del armado de cimentación.
Valores típicos de coeficientes de balasto K30
El estudio geotécnico de un terreno nos debe aportar una rigidez del mismo denominada K30, que es la rigidez del terreno ante una placa de 30x30cm. Este coeficiente de balasto K30 puede expresarse en kg/cm3 o en MN/m3.
Para una aproximación general a los valores típicos del K30 en los diferentes suelos, el CTE DB SE C nos aporta la tabla D.29, que a continuación reproducimos:

Aplicación a un caso práctico del cálculo de módulo de balasto
Ejemplo práctico para cálculo de módulo de balasto de una zapata rectangular 1,20m x 1,50m:
Supongamos que tenemos un terreno arcilloso que presenta un K30=4kg/cm3 (equivalente a un K30=40MN/m3)
Para el cálculo del coeficiente de balasto de una zapata rectangular, Ks, aplicaremos la fórmula que expresa la normativa, que es:
Ks, rectangular= (2/3)x Ks, cuadrada [1+b/(2L)]
Siendo:
- L: lado mayor de la zapata, expresado en metros
- b: lado menor de la zapata, expresado en metros
- Ks, cuadrada para terrenos cohesivos (arcillas)= K30 x [0,30/b]
- Ks, cuadrada para terrenos granulares (arenas)= K30x [(b+0,30)/(2b)]2
Siendo así, y dado que para el cálculo del Ks, cuadrada aplicaríamos la fórmula de suelos cohesivos, el Ks final para la zapata de 1,20 x 1,50m resultaría ser:
- Ks, cuadrada para terrenos cohesivos (arcillas)= K30 x[0,30/b]→Ks,c=10MN/m3
- Ks, rectangular= (2/3)x Ks, cuadrada [1+b/(2L)]→Ks,r =10MN/m3 → Ks, r= 9,3MN/m3
Asumiendo que la carga Q que soporta la zapata sea de 1,5 kg/cm2 (o lo que es lo mismo, 150 kN/m2), aplicando la fórmula inicial:
Ks=q/s→ s=q/Ks
Obtendremos el asiento final de la zapata, que resultará ser de s = 1,6 cm.




¿Qué pasa cuando el módulo del tipo de suelo que necesito encontrar es el agua?
Hola Oriana: Nos planteas una pregunta interesante desde un punto de vista teórico, y que además, puede ser de ejemplo sencillo para poder interpretar exactamente qué es el módulo de balasto. Este es la relación entre una tensión y la deformación o asiento que produce. El módulo de balasto del agua no sería 0, como inicialmente intuimos, sino que sería igual a su peso específico, dado que una presión de 9800 N/m3 daría como resultado la bajada de un metro exacto (punto en el que se equilibraría la presión aplicada superficialmente, desde arriba, y la inferior que ejercería el agua). ¡Gracias a Berta por su aportación!
No es cierto que el módulo de balasto del agua sea 0. Es 9800 N/m2 (su peso específico) que es la fuerza con la que empuja hacia arriba. Por algo el módulo de balasto tiene unidades de peso específico, porque se asimila el terreno a un líquido con una densidad enorme.
Gracias por tu aportación Berta, un placer poder contar con lectores críticos que nos señaléis los puntos débiles de nuestros posts (o de los comentarios que hagamos). ¡Comentario corregido y actualizado!
estimados, se puede hallar el modulo de balasto con una placa de 60 cm.?
Hola Luis,
Sí, tienes que calcular el módulo de balasto como si fuese para una zapata de 60x60cm.