Building rehabilitation sometimes requires to use beams that are not found in standard shapes, unique pieces that we usually create by means of adding steel plates. Before developing a complete structural model, we should err on the side of caution and check that specific shape.
One of the most important features we need to know is the Section Modulus of the beam’s cross section (and more specifically: the elastic section modulus – S, or Wel in Eurocodes-). The main purpose of getting S (or W) is that it is a very simple way of calculating the flexural resistance of that beam.
And as the Section Modulus is simply defined as S = I / y, being I the area moment of inertia (or the second moment of the area) and y the distance from the centroid or neutral axis to the furthest point of that section, we just need to discover the value of I.
I_x = ʃ y^2 dA \text{ and } Iy = ʃ x^2 dASteiner’s theorem allows us to get it working with smaller regular pieces. The area moment of inertia of a shape related to a certain Z’ axis is equal to the area moment of inertia of that shape, related to its own Z axis (the one passing through the body’s center of mass) plus a product of the area and the distance between the two axis:
I_x = ∑ I_x,i+ ∑(Ai \ x \ di^2)
So if we get the centroid of the complete shape, we can have its area moment of inertia by adding every piece’s I related to this new axis :
I_x = ∑ I_x,i+ ∑(Ai \ x \ di^2)
Once we get it, we just need to divide it between the distance to the furthest point to know S.
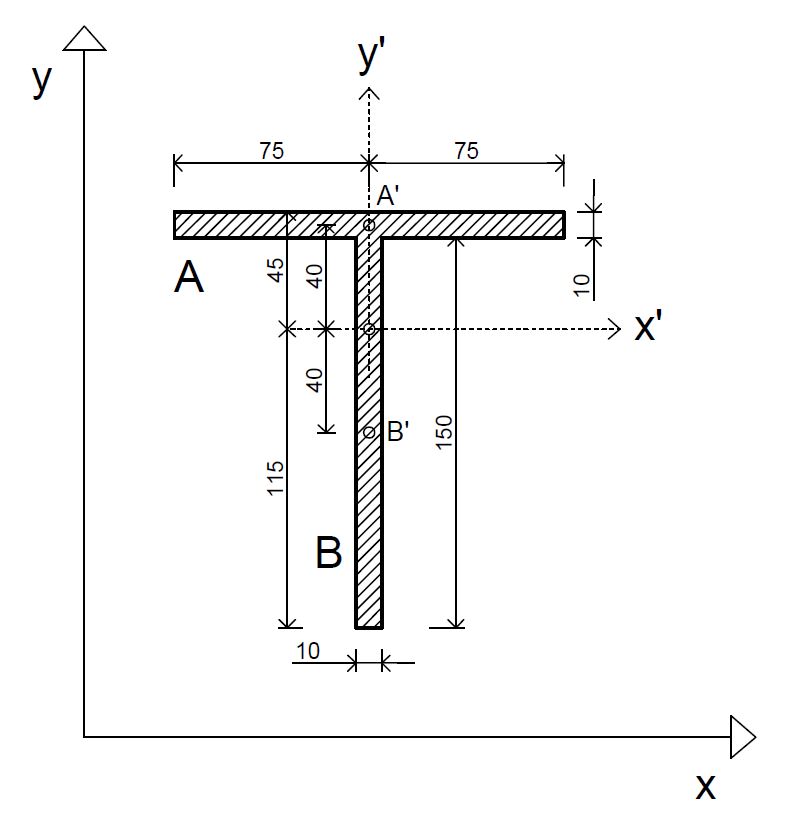
Example: Creation of a T section adding two plates of 150 x 10 mm
I_x = ∑ I_x,i+ ∑(Ai \ x \ di^2)
I_a = bh^3/12 = 12500 mm^4 \text{ } Aa \ x \ da^2 = 2400000 mm^4
I_b = bh^3/12 = 2812500 mm^4 \text{ } Ab \ x \ db^2 = 2400000 mm^4
\text{So }I_x = 7625000 mm^4
\text{And then: }W_{sup} = 169444 mm^3 \text{ } W_{sup} = 66304 mm^3
