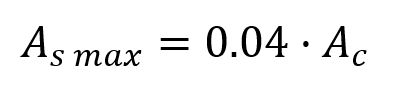Los pilares, al ser elementos que trabajan sometidos a compresión, son susceptibles de sufrir pandeo. El código estructural establece las condiciones para saber si, a la hora de dimensionar los pilares de hormigón, se debe tener en cuenta el efecto del pandeo o si puede despreciarse.
Para ello hay que comparar la esbeltez mecánica de la pieza con su esbeltez límite, y dependiendo del resultado, actuar en consecuencia.
Longitud de pandeo en elementos individuales
En primer lugar se debe hallar la longitud de pandeo del elemento a estudiar. En caso de tratarse de un elemento aislado utilizaremos la figura A19.5.7 del Código Estructural para determinar L0 =α * Lreal
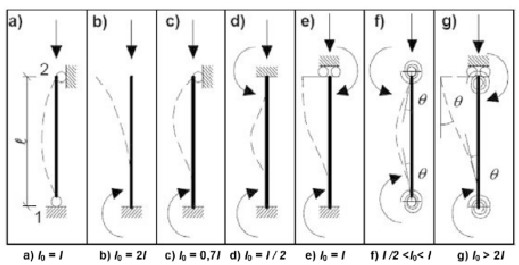
Cálculo de longitud de pandeo en pilares dentro de pórticos
En caso de tratarse de pórticos, se comienza distinguiendo entre pilares de pórticos traslacionales e intraslacionales. Esta diferencia altera la propia longitud de pandeo del pilar de estudio: L0 =α * Lreal
Para elementos de pórticos intraslacionales:
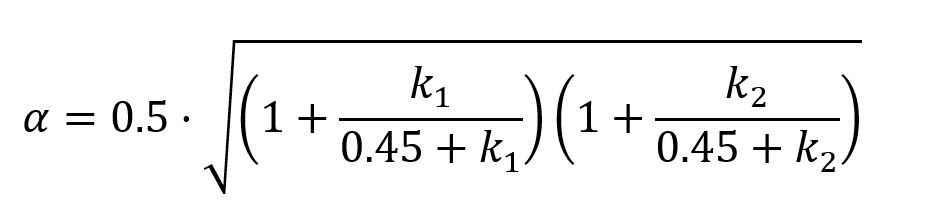
Y para elementos de pórticos traslacionales:
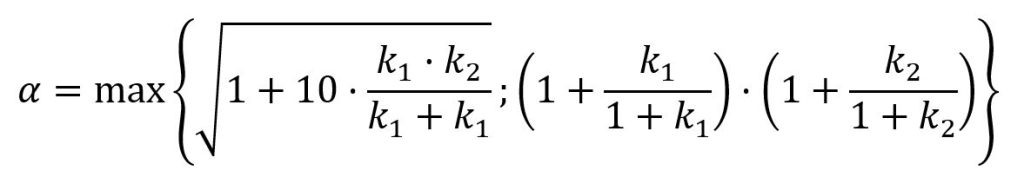
donde k es la flexibilidad en cada uno de los extremos del pilar (cabeza y pie). Así, podemos calcular k como señala el Código Estructural en su fórmula del apartado 5.8.3.2, o de manera simplificada:
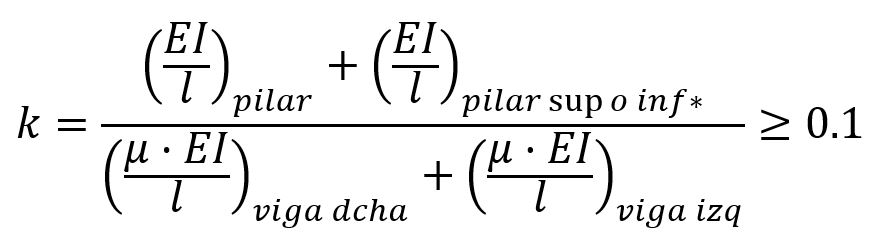
* Si queremos estudiar el valor de k en la cabeza del pilar de estudio (EI/L)pilar sup o inf se refiere a los valores del pilar situado encima del pilar de estudio, si lo hubiese.
* Si queremos estudiar el valor de k en el pie del pilar de estudio (EI/L)pilar sup o inf se refiere a los valores del pilar inmediatamente inferior al pilar de estudio.
El valor de μ depende del tipo de unión viga-pilar. Si se trata de un nudo rígido, muy habitual en pórticos de hormigón armado, el valor de μ será de 4, mientras que si se trata de un nudo articulado será de 3.
Por último, si no existen pilares encima o debajo, o si no existiesen vigas a izquierda o derecha de la cabeza o pie del pilar de cálculo, habrá valores de la ecuación que sean nulos. Esta situación podría llegar al extremo en el que k nos devolviese un valor completamente nulo. En ese caso, ante la imposibilidad de lograr un empotramiento perfecto, se recomienda no adoptar valores de k inferiores a 0.1.
Esbeltez mecánica
La esbeltez mecánica se calcula directamente mediante λ = L0 / i siendo i el radio de giro del pilar, tal que:
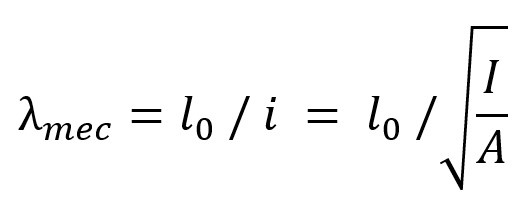
Siendo I el momento de inercia y A el área de la sección del pilar.
Esbeltez límite
La esbeltez límite se calcula tal que:
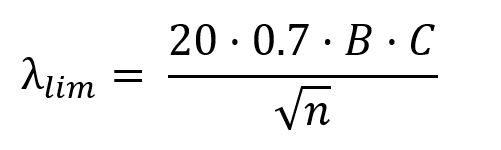
donde B es un coeficiente que depende de la cuantía mecánica de la armadura. Si conocemos la armadura del pilar, obtendremos B tal que:
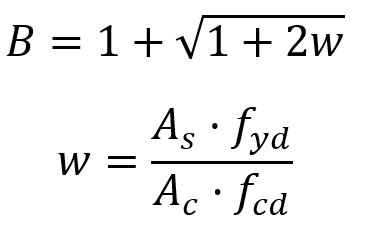
Y si no la conocemos, que suele ser un caso habitual ya que puede que aún nos encontremos dimensionando el propio pilar, adoptaremos un valor tal que B=1.1.
C dependerá de la traslacionalidad del pórtico en el que se encuentra el pilar. En caso de tratarse de un pórtico traslacional, se tomará un valor de C=0.7. En caso de tratarse de uno intraslacional, se tomará un valor tal que C = 1,7 – M01/M02
Los valores de M01 y M02 se obtendrán a partir de los esfuerzos de axial de compresión y momento flector que sufre el pilar, de tal forma que:
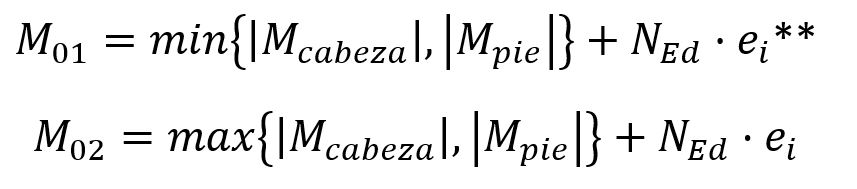
** M01 se tomará negativo si el valor del momento en la cabeza y en el pie del pilar generan tracciones por las caras opuestas del pilar. El valor de ei se calcula tal que: ei = L0 / 400
Una vez obtenidos M01 y M02 obtendremos el valor de C.
Tras ello, solo queda calcular n para finalmente hallar el valor de la esbeltez límite.
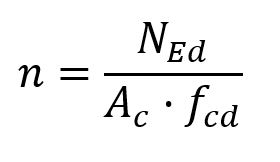
Comparativa esbeltez mecánica y límite
Una vez obtenidos todos los valores anteriormente descritos, se procede a comparar los valores de esbeltez mecánica y esbeltez límite para verificar si se ha de tener en cuenta el valor del pandeo en el dimensionamiento del pilar o no. Tras realizar dicha comparación, obtendremos dos posibles resultados:
1) λmec < λlim : No se tiene en cuenta el pandeo
En este caso, se puede dimensionar la armadura del pilar mediante los valores de NEd y MEd. NEd es directamente el valor de la carga de compresión que sufre el pilar mientras que MEd es el valor del momento de cálculo, que se calcula tal que:
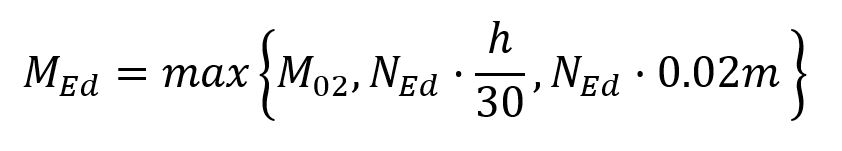
2) λmec > λlim : Se tiene en cuenta el pandeo
Para esta situación, el código estructural establece dos métodos para el cálculo simplificado de la comprobación del pandeo. En este caso, para el cálculo a flexocompresión, se explicará la resolución mediante el método basado en la curvatura nominal. Para ello, de cara al valor de compresión a utilizar, se tendrá en cuenta directamente el valor de NEd. Para el valor del momento, se obtendrá momento de cálculo MEd que se calculará como la suma del momento de primer orden M0e y un momento nominal M2 de segundo orden.
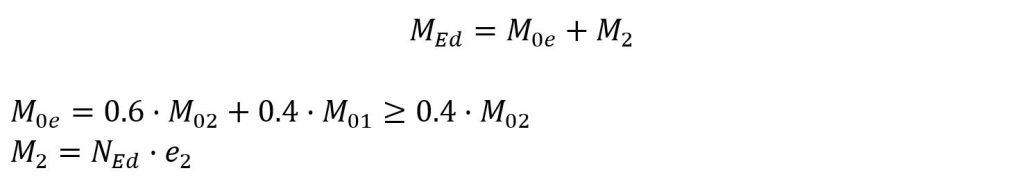
e2 es la flecha de la curva que adopta el pilar en el pandeo, y se calcula tal que:
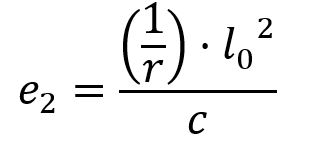
donde 1/r es la curvatura del pilar, tal que:
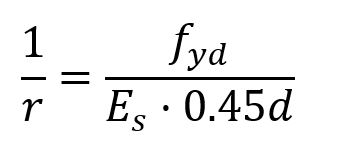
y c es un coeficiente que depende de la propia curvatura, cuyo valor será c=10 de forma general y c=8 si el momento es constante en el pilar.
Una vez hallados todos los valores, se dimensionará la armadura a flexocompresión con los valores de NEd y MEd, siendo NEd el valor del esfuerzo axial de compresión, y MEd
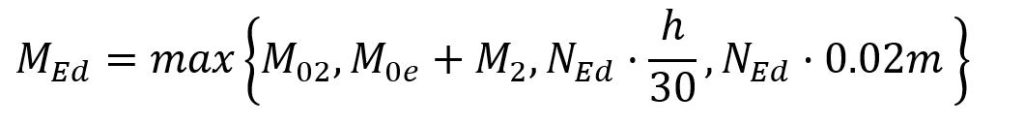
Dimensionamiento de armadura del pilar
Los pilares habrán de armarse de modo que cubran las solicitaciones especificadas. Además el código estructural establece unos valores mínimos. Para el caso de elementos sometidos a compresión simple y armados simétricamente, el área mínima de sección de armadura es:
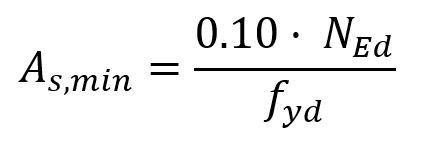
Y, en el caso de flexión compuesta, la armadura principal de tracción o compresión debe cumplir los siguientes valores mínimos:
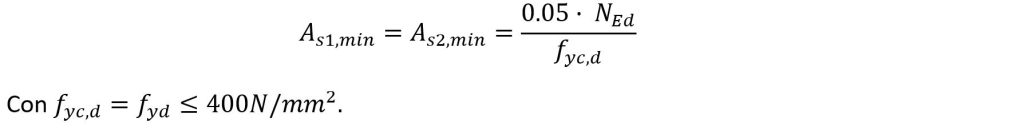
Y como valor máximo, el área de la armadura longitudinal no podrá superar: